Ayudantía 2: Correlación de Pearson

Estadística Correlacional

Equipo de Ayudantes

15 de octubre de 2025

Índice

  1. Covarianza

  2. Correlación de Pearson

  3. Nube de puntos o Scatterplot

  4. Ejercicio

Apretar Cápsula !!! para ingresar a la grabación

Covarianza

La covarianza es una medida de asociación entre variables basada en la variabilidad de cada una de ellas, pero su valor no es interpretable directamente: a pesar de que mida la relación/asociación lineal entre dos variables, solo indica la dirección (positiva o negativa), la magnitud depende de las unidades de las variables.

Correlación de Pearson

Medida estandarizada de covarianza.

Correlación de Pearson
Categoría Requisito
Tipo de variables Intervalar/Razón + Intervalar/Razón
Interpretación Asociación lineal entre variables que indica sentido y fuerza de la asociación entre -1 a 1
Dirección Determinada por el signo del valor: positiva o negativa
Intensidad de efecto Criterios de Cohen (1988, 1992): muy pequeño (menor a 0.1), pequeño (entre 0.1 a 0.3), moderado (entre 0.3 y 0.5), grande (mayor a 0.5)
Significancia Como mínimo 95% de confianza (p < 0.05)

Importante: refiere a asociación, NO a causalidad.

¿Cómo se calcula?

Para efectos prácticos, ocuparemos el siguiente código de R para calcular este tipo de correlación:

cor.test(basededatos$variable1, basededatos$variable2, method = "pearson")

Así, obtendremos el valor-t, valor-p, el intervalo de confianza al 95% y el valor de la correlación.

Nube de puntos o Scatterplot

Es una representación gráfica de la asociación de dos variables, donde cada punto representa el valor de cada caso en cada una de las variables.

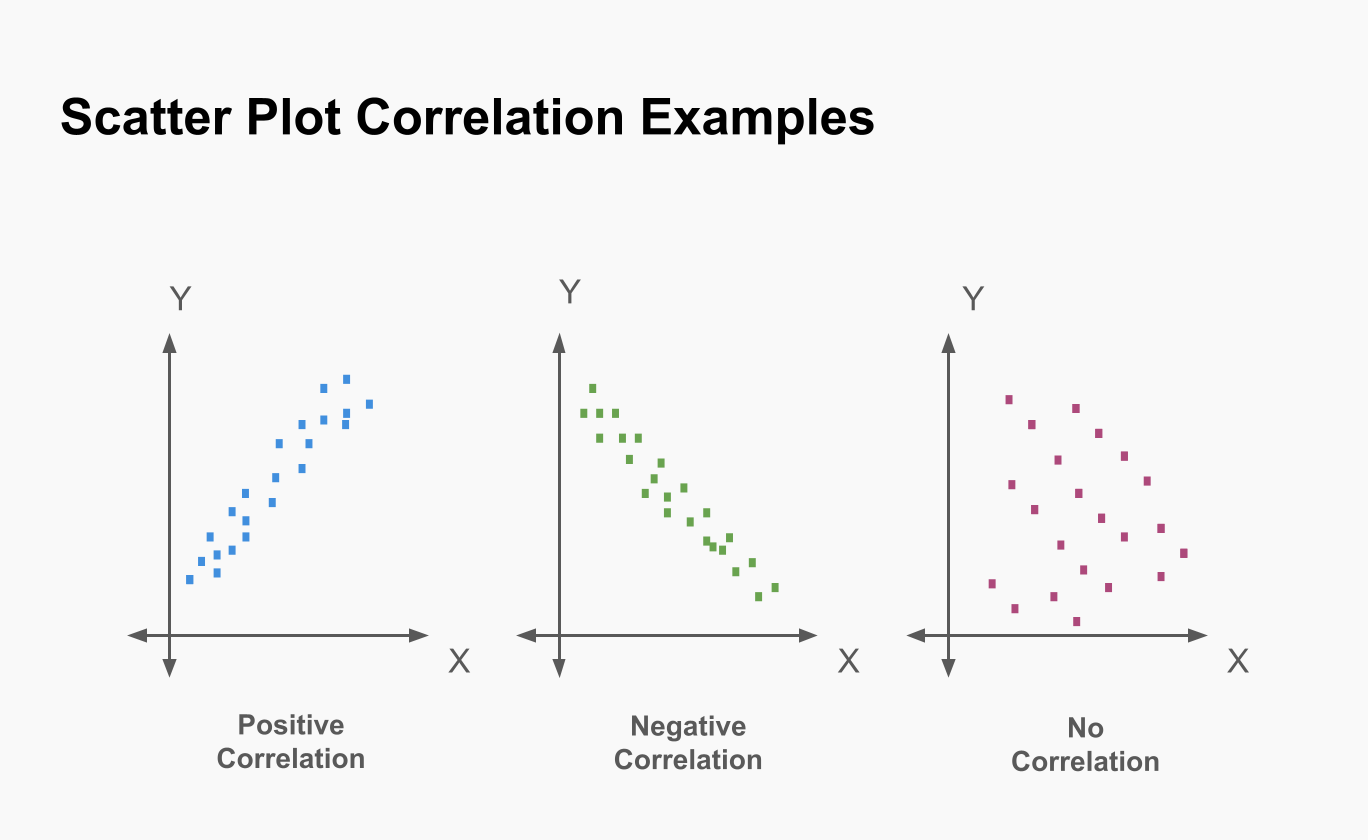
sjPlot::plot_scatter(data = basededatos, x = variable1, y = variable2)

Ejercicio práctico

¿En qué medida se relacionan los ingresos (en pesos) de las personas con sus niveles de autoritarismo?

pacman::p_load(tidyverse, # Manipulacion de datos
               car, # Recodificar
               sjPlot, # Tablas y graficos
               sjmisc, # Descriptivos
               kableExtra, # Tablas
               psych, # Bivariados
               corrplot, # Graficos correlacioj
               broom) # Varios

options(scipen = 999) # para desactivar notacion cientifica
rm(list = ls()) # para limpiar el entorno de trabajo

load(url("https://github.com/cursos-metodos-facso/datos-ejemplos/raw/refs/heads/main/dataset4.RData")) # base de datos a utilizar

Ejercicio práctico: preguntas orientadoras

Antes de resolver el ejercicio, es importante tener las siguientes preguntas en mente:

  • ¿Cuál es la naturaleza de nuestras variables?

  • ¿Qué queremos saber de nuestras variables?

  • ¿Qué medida estadística nos permite responder la pregunta?

Ejercicio práctico: variables a utilizar

Se usarán las variables ingresos y autoritarismo de la base de datos anteriormente descargada. Para conocer los descriptivos de las variables se puede usar summary:

summary(dataset4$ingresos)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
 110000  450000  680000  840318  920000 3000000     150 
summary(dataset4$autoritarismo)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
   4.00   41.00   52.00   52.28   59.00  100.00      10

Ejercicio: resolución

Se usará cor.test para calcular la correlación de Pearson entre ambas variables:

cor.test(dataset4$ingresos, dataset4$autoritarismo, method = "pearson")

    Pearson's product-moment correlation

data:  dataset4$ingresos and dataset4$autoritarismo
t = 37.907, df = 838, p-value < 0.00000000000000022
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7684251 0.8184034
sample estimates:
      cor 
0.7947577

Ejercicio: resolución

Gráficamente, la correlación anteriormente calculada se vería de la siguiente forma:

sjPlot::plot_scatter(data = dataset4, x = ingresos, y = autoritarismo)

Ejercicio: interpretación

Una buena interpretación debe contener los siguientes elementos:

  • Dirección e intensidad (mencionando valores obtenidos y criterios utilizados).

  • Interpretación “en fácil”: “a medida que x aumenta, y aumenta/disminuye”.

  • Significancia estadística (se rechaza o no hipótesis nula).

Si se pide justificar el uso de un coeficiente de correlación en específico, en general se explica por el nivel de medida de las variables.

Ejercicio: interpretación

Se empleó el coeficiente de correlación de Pearson debido a la naturaleza de las variables, en tanto los ingresos en peso y el nivel de autoritarismo corresponden a variables númericas de razón. El coeficiente da cuenta de una relacion positiva y grande, siguiendo los criterios de Cohen (1988) (r = 0.79). Es decir, a medida que aumentan los ingresos de las personas, también aumentan sus niveles de autoritarismo. La relación es estadísticamente significativa (p < 0.001), por ende es posible rechazar H0 sobre no asociación entre variables, entregando evidencia a favor de una relación entre ambas variables con un 99.9% de confianza.

Conclusión

  • La correlación de Pearson es una medida estandarizada de covarianza, que mide de manera lineal la relación entre dos variables numéricas.

  • Para graficarla, se utilizan gráficos de nube de puntos.

  • Revisar clases Bivariada 1 y Bivariada 2 para mayor información.

Gracias por su atención !